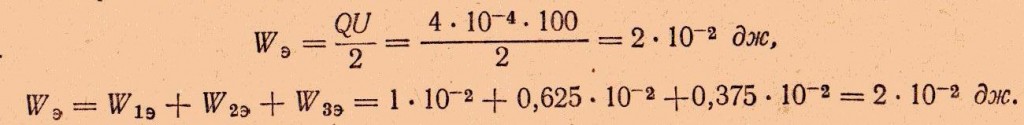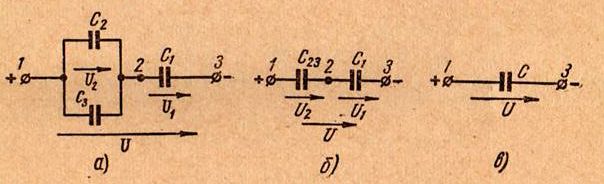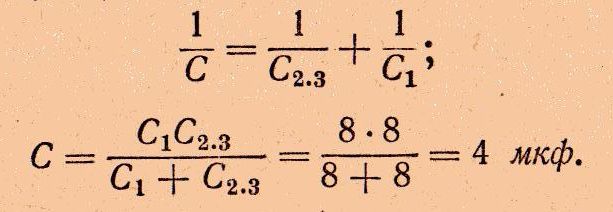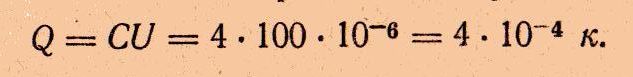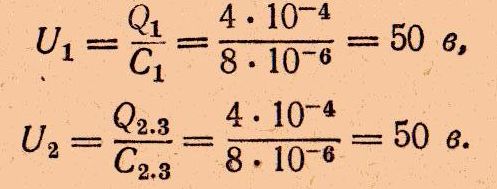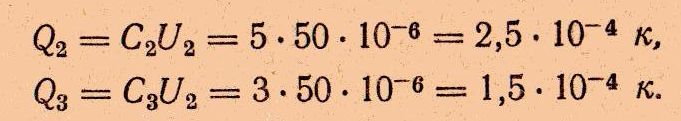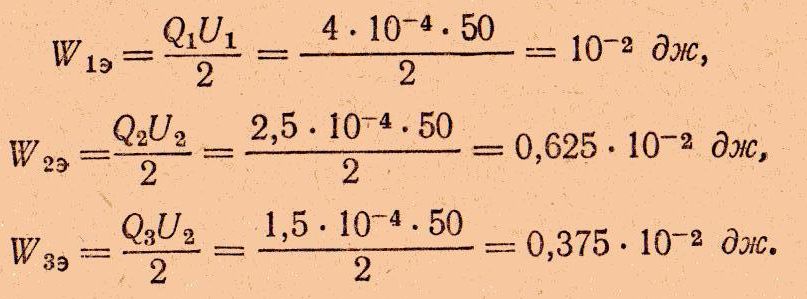Задача 11

Определить заряд, напряжение и энергию каждого конденсатора с идеальным диэлектриком в схеме Рис.1, а, если емкости их С₁ = 8 мкф, С₂ = 5 мкф, С₃ = 3 мкф, а общее напряжение U = 100 в.

Рис.1

Решение:

Такого типа задачу нужно решать, начав с определения эквивалентной емкости. Конденсаторы С₂ и С₃ соедены паралельно относительно точек 1, 2 схемы. Заменим эти два конденсатора одним с эквивалентной емкостью С_2,3 (Рис.1, б). Получим:

В новой, упрощенной схеме между точками 1, 2 вместо двух конденсаторов включен один С_2,3. Емкость его равна емкости двух конденсаторов С₂ и С₃. При такой замене распределение напряжений в схеме не изменилось, не изменился и общий заряд в системе.

По отношению к точкам 1 и 3 конденсаторы С_2,3 и С₁ соединены последовательно.

Заменим эти два конденсатора одним с эквивалентной емкостью С, которая является общей емкостью между точками 1 и 3 в схеме Рис.1,а. После замены получим схему Рис.1, в, где к зажимам источника напряжения (точки 1, 3) подключен один конденсатор.

Согласно известным формулам, имеем:

Общий заряд системы конденсаторов в схеме Рис.1, а

Общий заряд системы равен заряду конденсатора С₁ и конденсатора С_2,3:

Напряжение U₂ является общим для конденсаторов С₂ и С₃. Заряды этих конденсаторов

Проверка:

Энергия электрического поля каждого конденсатора:

Энергия всей системы конденсаторов