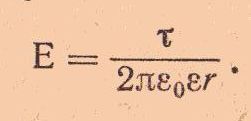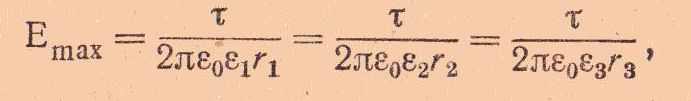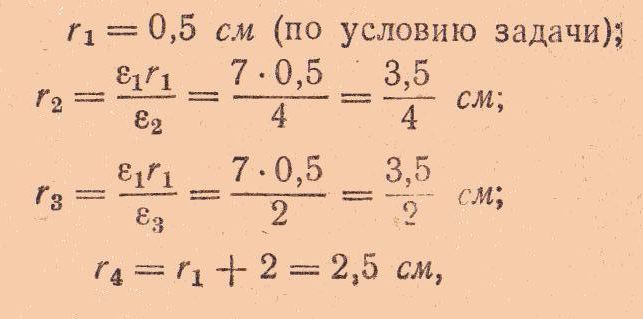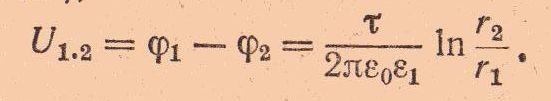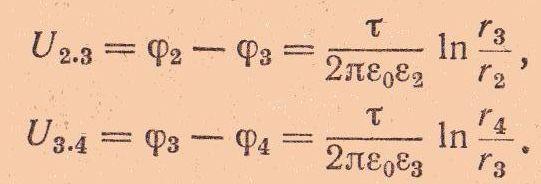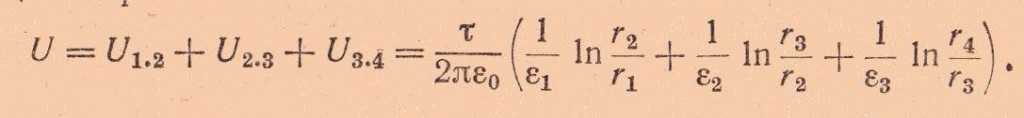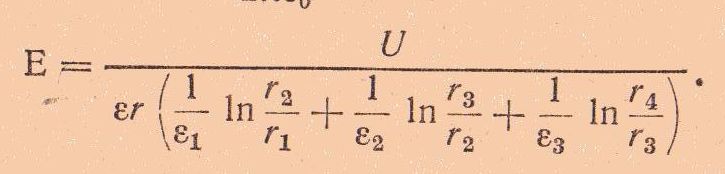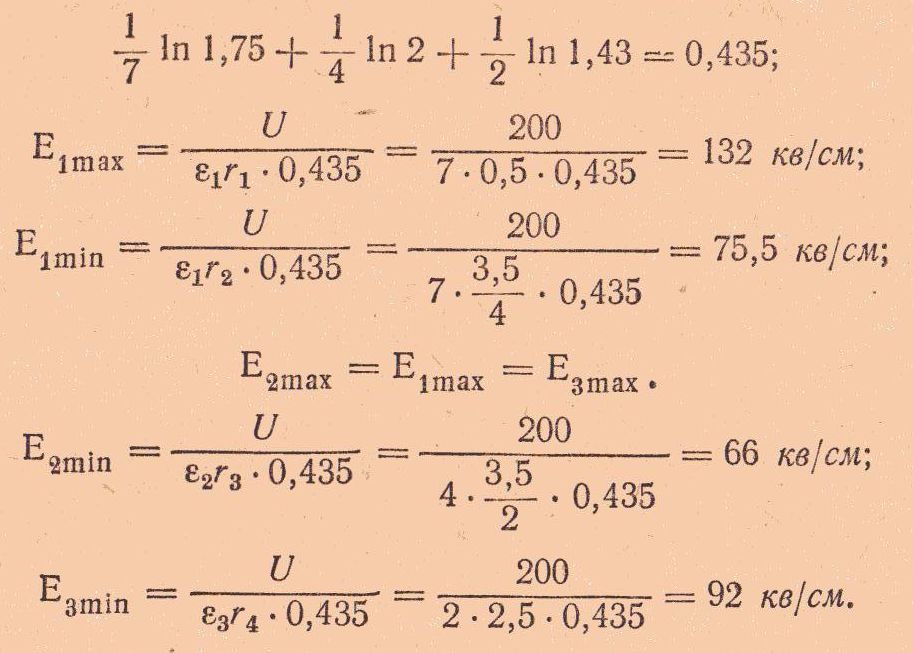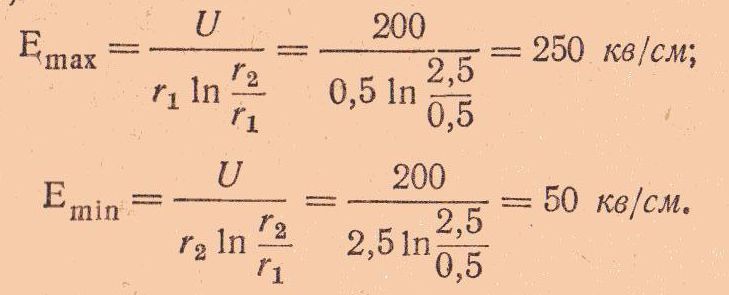Цилиндрический конденсатор с радиусом внутреннего цилиндра r1 = 0,5 см включен на рабочее напряжение 200 кв (Рис.1). Изоляция конденсатора, толщина которой 2 см, выполнена тремя слоями диэлектриков с одинаковой электрической прочностью Епр = 200 кв/см, но с разными диэлектрическими проницаемостями: первого слоя ε1 = 7, второго ε2 = 4, третьего ε3 = 2.
Определить максимальную и минимальную напряженность поля в каждом слое диэлектрика, если конструкция конденсатора выполнена с условием наилучшего использования изоляции. Построить график распределения напряженности поля вдоль радиуса поперечного сечения конденсатора.
Рис.1
Решение:
Напряженность поля будем определять по известной формуле, пренебрегая искажением поля у краев конденсатора:
Поскольку электрическая прочность диэлектриков одинакова, конструкция изоляции будет правильной, когда максимальная напряженность поля во всех слоя одинакова:
или
где r1, r2, r3 — внутренние радиусы слоев.
Определим из этого условия внутренние радиусы слоев:
Согласно известной формуле:
Аналогично
Общее напряжение
Тогда, из известной формулы следует ![]() для любого слоя. Поэтому
для любого слоя. Поэтому
Эта форму пригодна для определения напряженности поля в любом слое, но при переходе через границу раздела нужно менять индексы у ε и r.
Определим величину, стоящую в знаменателе в скобках:
Между Emax и Emin напряженность поля изменяется по гиперболе. График напряженности поля показан на Рис.1.
Для сравнения определим Emax и Emin в том случае, если изоляция конденсатора выполнена однослойной. Получим такие выражения:
Вывод. При выполнении изоляции в один слой фактическое значение напряженности поля Emax больше электрической прочности диэлектрика. Изоляция будет пробита.