Symbolic method of operations with vector quantities are based on a very simple idea: every vector display on two components: one horizontal, going on the x-axis and the second is the vertical ordinate going. In this case, all horizontal components are on the same line, and they can be added using a simple algebraic addition, similarly folded and vertical components.
With this approach, in General, produces two result components — horizontal and vertical, which always are to each other under the same angles equal to 90°.
For those drivers can find their way, i. e. to the geometric addition. Components at right angles to represent the legs of a triangle a right triangle, and their geometric sum is the hypotenuse.
You can also say that the amount of geometry is numerically equal to the diagonal of the parallelogram, built on pillars on both sides. If the horizontal component of the label and vertical-ÀB AG, the geometric sum (1)
Find the geometric sum of rectangular triangles is much easier than kosougolnyh. It is easy to see that (2)
превращается в (1) если угол между составляющими составляет 90°. Поскольку cos 90 = 0, последний член в подкоренном выражении (2) исчезает, вследствие чего выражение резко упрощается. Обратим внимание на то, что перед словом “сумма” обязательно следует добавлять одно из трех слов: “арифметическая”, “алгебраическая”, “геометрическая”.
Fig.1.
Слово “сумма” без указания, какая именно, приводит к неопределенности, а в ряде случаев и к грубым ошибкам.
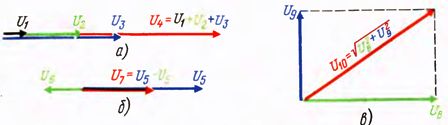
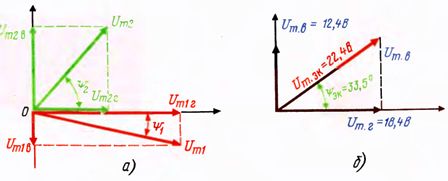
We remind that the resulting vector is equal to the arithmetic sum of the vectors in the case where all vectors are on the same line (or parallel to each other) in the same direction. In this case all vectors have a plus sign (fig. 1, a).
If the vectors are on the same line, but are directed in opposite directions, their resultant is equal to the algebraic sum of the vectors, in which case some members have a plus sign, while others are negative.
For example, in the figure. 1, b = U4 U6-U5. You can also say that an arithmetic sum of use in cases when the angle between the vectors is zero, algebraic, when angles represent 0 and 180°. In all other cases, the addition of the produce vector, i.e. define the geometric sum (fig. 1, b).
Sample. Define the parameters of an equivalent sinusoid chain fig. 2, and the symbolic method.
Solution. Draw the vectors Um1 Um2 and decompose them into components. From the drawing it is seen that each horizontal component represents the value of the vector multiplied by the cosine of the phase angle, and the vertical value of the vector multiplied by the sine of the phase angle. In this case
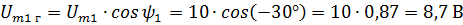
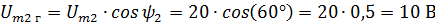
Fig.2.
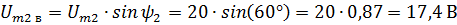
It is obvious that general horizontal and vertical components are equal to the algebraic sums of relevant constituents. In this case,
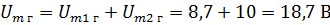
The resulting components show in Figure 1. 2. Define the value for the Um Let's calculate the geometric sum of two components:
Define equivalent phase angle ψjek. From Fig. 2, b shows that the ratio of horizontal to vertical component represents the tangent of the phase angle equivalent.
From where
Thus, the resulting sinusoid has amplitude 22.4 in the initial phase, 33.5° c in the same period, which were components. Note that you can only fold sinusoids with the same frequency as when adding sine curves with different frequencies, the resulting curve ceases to be sinusoidal, and all concepts, prilozhimye only to the harmonic signals in this case, the unlawful.
Let us follow again the whole chain of transformations that have to do with mathematical descriptions of harmonic signals form when performing various calculations.
First time functions replace vector images, then every vector display on two mutually perpendicular components, and then calculate the horizontal and vertical components separately and finally define values the resulting vector and its initial phase.
This way of calculation eliminates the need to graphically fold (and in some cases do more complicated operations, such as multiplying, dividing, extracting roots, etc.) sinusoidal curves and calculations with formulas kosougolnyh triangles.
However, count separately the horizontal and vertical components of operation quite bulky. When such calculations very convenient is the mathematical apparatus, with which you can calculate both components at once.
Уже в конце прошлого века был разработан метод, позволяющий одновременно производить расчеты над числами, отложенными на взаимно перпендикулярных осях. Числа, откладываемые по горизонтальной оси, назвали вещественными, а по вертикальной оси — мнимыми. При расчетах этих чисел к вещественным добавляют множитель ± 1, а к мнимым — ±j (читается “жи”). Числа, состоящие из вещественной и мнимой частей, назвали комплексными, а метод расчетов, выполняемых с их помощью — символическим.
Поясним термин “символический”. Те функции, которые подлежат расчету (в данном случае гармонические), являются оригиналами, а те выражения, которыми заменяют оригиналы — изображениями или символами.
When using symbolic method, all calculations produce originals themselves over and over their symbols (images), which in our case are the corresponding complex numbers, since produce operations on images It is much easier, than by the originals.
After all image manipulation on the resulting image to write original, matching its resulting image. Symbolic method produce the vast majority of the calculations in electrical circuits.
