Эксперимент 9. Измеряем время с помощью конденсаторов

Вам понадобятся:
1. Сетевой адаптер, макетная плата, провод, кусачки для отрезания проводов и инструменты для снятия изоляции.
2. Мультиметр.
3. Кнопочный переключатель без фиксации, однополюсный однопозиционный (SPST). Количество — 1 шт.
4. Резисторы и электролитические конденсаторы в ассортименте.

В эксперименте 8, когда вы устанавливали конденсатор параллельно обмотке реле, конденсатор заряжался практически мгновенно перед тем, как разрядиться через обмотку реле. Если бы вы последовательно к конденсатору добавили резистор, то длительность разряда конденсатора, безусловно, возросла бы. Изменяя длительность разряда конденсатора, вы можете измерять время, что является очень важным.
Снимите все компоненты с вашей макетной платы эксперимента 8 и используйте ее для сбора другой очень простой схемы, монтаж которой показан на рис. 1, где C1 — электролитический конденсатор емкостью 1000 мкФ, R1 — резистор 100 кОм, R2 — резистор 100 Ом и S1 — кнопочный переключатель, который вы уже использовали ранее. Установите на вашем мультиметре режим для измерения постоянного напряжения, подсоедините наконечники измерительных щупов к контактам конденсатора и нажмите на кнопку. Вы должны увидеть, как прибор будет увеличивать показания по мере того, как конденсатор будет накапливать заряд. (Это легче сделать с мультиметром, который не имеет автоматического определения диапазона, поскольку вам не придется ждать до тех пор, пока тестер определит используемый диапазон). Резистор R1 будет замедлять время заряда конденсатора.

Рис. 1. Посмотрите, как конденсатор накапливает заряд (увеличивает напряжение на выводах) после того, как вы нажали кнопку. Замените резистор R1 резистором другого номинала, разрядите конденсатор, замкнув его выводы резистором R2, и повторите процесс измерения. S1 — кнопочный переключатель типа Выкл. (Вкл.); R1 — резистор 100 кОм; R2 — резистор 100 Ом; C1 — конденсатор 1000 мкФ.

Отпустите кнопку, отсоедините ваш мультиметр и разрядите конденсатор, замкнув его выводы резистором R2 в течение одной или двух секунд. Теперь замените резистор R1, установив резистор номиналом 50 кОм, и повторите измерение. Тестер должен завершить отсчет за время, по меньшей мере, в два раза меньшее, чем в предыдущем варианте схемы.

Напряжение, сопротивление и емкость

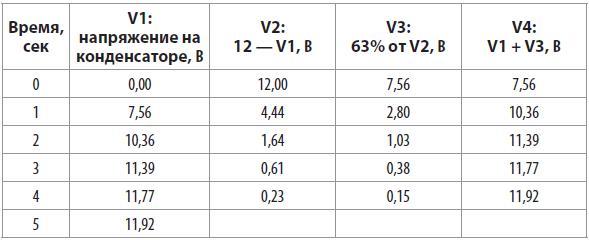
Представьте, что резистор, имеющий некоторое сопротивление (resistance), это водопроводный кран, а конденсатор это некоторый надувной баллон (balloon) — емкостью (capacitance), которую вы хотите заполнить водой. Когда вы закрываете кран до такой степени, что через него течет маленькая струйка, емкость будет наполняться дольше. Тем не менее медленный поток воды все равно заполнит всю емкость, если вы будете ждать достаточно долго (предполагая, что баллон не будет разорван) и процесс закончится, когда давление внутри емкости не станет равным давлению (pressure) внутри трубопровода, который подает воду через кран (рис. 2).

Рис.2. Когда кран закрыт наполовину, емкость будет заполняться дольше, но все равно она может «принять» такое же количество воды, которое будет равно ее объему и которое создаст давление, равное давлению внутри трубопровода

Аналогичное происходит и в нашей схеме, если вы ждете достаточно долго, то напряжение на выводах конденсатора должно достичь того же значения, которое имеет источник напряжения. В цепи с напряжением питания 12 В конденсатор должен достичь напряжения 12 В (хотя это в итоге займет гораздо больше времени, чем вы думаете).
Это может показаться удивительным, поскольку ранее вы усвоили, что когда вы подаете напряжение на один конец резистора, то вы получаете меньшее напряжение по мере прохождения тока через него. Почему резистор передает полное напряжение, когда соединен с конденсатором?

Забудьте на некоторое время о конденсаторе и вспомните, как вы тестировали два одинаковых резистора с сопротивлением 1 кОм, соединенных последовательно. В этой ситуации каждый резистор представляет собой половину общего сопротивления цепи, поэтому на каждом резисторе падает половина общего напряжения цепи. Если вы подсоедините наконечник измерительного щупа черного цвета, подключенного к общей клемме (COM) вашего мультиметра, к отрицательному выводу источника напряжения, а затем другим щупом красного цвета, подключенным к гнезду для измерения напряжения (V), коснетесь центральной точки цепи, расположенной между двумя резисторами, то вы получите результат измерения, равный 6 В (рис. 3).

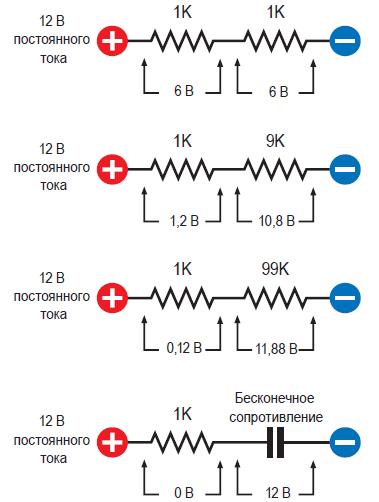Рис. 3. Когда два резистора соединены последовательно, то на большем сопротивлении будет падать большее напряжение, чем на меньшем. Если резистор будет иметь бесконечно большое сопротивление (как это будет в случае конденсатора), то меньшее сопротивление больше не будет давать какой-либо вклад в падение напряжения, а напряжение на его выводах будет одинаковым ( т. е. между этими точками разность потенциалов будет равна нулю).

Теперь предположим, что вы убрали один резистор номиналом 1K (на рисунке он справа) и заменили его резистором 9K. Общее сопротивление цепи теперь станет равным 10K и поэтому на резисторе номиналом 9K будет падать 90% общего напряжения 12 В. Оно будет равным 10,8 В. Вы должны проверить это с помощью своего мультиметра. (Вряд ли вам удастся найти резистор с сопротивлением 9K, поскольку это нестандартное значение. Замените его ближайшим по величине сопротивлением, которое вы найдете.)
Затем предположим, что вы убрали резистор номиналом 9K и заменили его резистором на 99K. Падение напряжения на нем станет равным 99% возможного напряжения или 11,88 В. Теперь вы можете заметить общую закономерность: чем больше сопротивление резистора, тем больше его вклад в падение напряжения.
Однако, как я уже отмечал ранее, конденсатор полностью блокирует все постоянное напряжение. Он может аккумулировать электрический заряд, но при этом никакого тока через него вы измеряете падение напряжения на резисторе. Внутреннее сопротивление мультиметра намного больше, чем величина сопротивления большинства резисторов. Однако следует помнить, что внутреннее сопротивление конденсатора почти равно бесконечности. В этом случае внутреннее сопротивление мультиметра уже будет иметь значение. Поскольку вы никогда не сможете иметь идеальный мультиметр, даже тогда, когда у вас будет идеальный конденсатор и резистор, ваш прибор всегда будет немного влиять на схему, и вы, наверняка, получите приблизительный результат измерения. Если же вы попытаетесь измерить напряжение на конденсаторе, который был заряжен, но в данный момент не подключен к какой-либо цепи, то вы увидите, что значение напряжения будет медленно уменьшаться, поскольку конденсатор будет разряжаться через подключенный мультиметр.

Теория

Постоянная времениВы можете удивиться, если узнаете, что существует способ точно предсказать время, в течение которого будут заряжаться различные конденсаторы, когда они подключены к различным резисторам. Существует ли формула для расчета этого?Естественно, ответ будет — «да», но способ, которым мы будем измерять это время, будет несколько замысловатым, поскольку конденсаторы не заряжаются с постоянной скоростью. Они достигают значения напряжения равного 1 В очень быстро, значения 2 В уже не так быстро, а 3 В еще медленнее и т. д. Вы можете представить себе электроны, накапливающиеся на пластине, людьми, которые прогуливаются в аудитории и которые ищут место для того, чтобы сесть. Чем меньше мест остается, тем больше людям нужно времени, чтобы найти их.

Величина, которая описывает это, называется «постоянная времени». Определение этой величины очень простое:

где τ — это постоянная времени; C — емкость конденсатора в фарадах, который заряжается через резистор сопротивлением R в омах.

Возвращаясь к цепи, которую вы только что тестировали, используем резистор на 1 кОм и конденсатор емкостью 1000 мкФ. Мы должны перевести эти значения в фарады и омы прежде, чем использовать их в формуле. Отлично, 1000 мкФ это 0,001 Ф и 1 кОм это 1000 Ом, поэтому формула будет выглядеть следующим образом:

τ= 1000 х 0,001

Другими словами, τ = 1 — вывод, который просто нельзя упростить еще больше для лучшего запоминания:
Резистор с сопротивлением 1 кОм, подсоединенный последовательно с конденсатором емкостью 1000 мкФ, имеет постоянную времени τ равную 1.
Означает ли это, что конденсатор будет полностью заряжен в течение 1 сек? Нет, все не так просто. τ — это постоянная времени, которая указывает время, нужное конденсатору, чтобы достичь 63% от напряжения, которое подается на него, если в начале процесса конденсатор был полностью разряжен, т. е. имел напряжение равное 0 В.
(Почему именно 63%? Ответ на этот вопрос слишком сложен для того, чтобы его объяснить в рамках этого эксперимента, и если вы хотите узнать больше о постоянной времени, то вам надо изучить дополнительную литературу. При этом вам надо быть готовыми разбираться в дифференциальных уравнениях.) Здесь приведено формальное определение для сведения в будущем:
Постоянная времени τ — это время, которое необходимо конденсатору, чтобы он зарядился до значения, равного 63% от разности между текущим напряжением на конденсаторе и напряжением подключенного источника питания. Когда τ = 1, конденсатор заряжается до значения 63% от полной величины в течение 1 сек. Когда τ = 2, конденсатор заряжается до значения 63% от полной величины в течение 2 сек. И т. д.
Что произойдет, если продолжить подавать напряжение? История повторится снова. Конденсатор зарядится на следующие 63% оставшейся разности между текущим значением напряжения и напряжением, которое будет к нему приложено.
Представим, что некто ест торт. Когда он первый раз кусает его и при этом еще голоден, то съедает 63% за одну секунду (рис. 4). В течение второго откусывания он не хочет выглядеть слишком жадным и съедает только следующие 63% от оставшейся части торта, и поскольку он уже не так голоден, ему потребуется столько же времени, сколько он потратил на поглощение первого куска. В течение третьего «подхода» он съедает еще 63% от оставшейся части торта и потратит на это тоже количество времени и т. д. Он ведет себя точно так же, как конденсатор, когда «поедает» электричество.

Рис. 4. Если наш гурман каждый раз съедает только 63% от торта, который в данный момент находится на тарелке, он «заряжает» свой желудок точно так же, как это делает конденсатор, когда заряжается. Не имеет значения, как много времени это займет, его желудок никогда не будет заполнен полностью.

Любитель тортов всегда будет оставлять что-то, что можно еще съесть, поскольку он никогда не отправляет в рот все 100% оставшегося торта. Точно также, как и конденсатор никогда не может зарядиться полностью. В идеальном мире, состоящем из идеальных компонентов, этот процесс будет продолжаться бесконечное время.
В реальном времени мы можем произвольно сказать:
После периода, равного 5 × τ, конденсатор будет заряжен практически полностью, и мы будем считать, что разница между имеющимся зарядом и полным зарядом ничтожно мала.
В табл. 1 приведен расчет (округлен до двух цифр после запятой), который показывает накопление заряда конденсатора в цепи с источником питания 12 В, когда постоянная времени равна 1 сек.

Таблица 1.
Здесь приведены пояснения к содержимому таблицы. V1 это текущее значение напряжения на конденсаторе в вольтах. Нужно вычесть это значение из напряжения источника питания (12 В), чтобы определить разность. Обозначим эту разность, как V2. Теперь возьмем 63% от V2 (это V3) и добавим это значение к текущему значению напряжения (V1) и получим результат, который обозначим V4. Это новое значение напряжения, до которого конденсатор зарядится через 1 сек, поэтому мы копируем это значение в следующую строку таблицы и оно становится новым текущим значением напряжения на конденсаторе V1.
Теперь повторим этот процесс снова и снова. На рис. 5 это показано в графической форме. Заметим, что через 5 сек конденсатор достигнет значения 11,92 В, что составляет 99% от напряжения источника питания. Это должно быть достаточно близко, чтобы удовлетворить любым требованиям, которые могут встретиться в реальной ситуации.

Рис.5. Конденсатор начинает заряжаться, начиная с напряжения 0 В. Через промежуток времени, равный постоянной времени, он добавит 63% от приложенного напряжения. После окончания второго периода такой же длительности будет добавлено еще 63% оставшейся разности напряжений и т. д.

Если вы хотите проверить эти цифры путем измерения напряжения на конденсаторе по мере его зарядки, то следует помнить, что поскольку ваш тестер «приворовывает» немного тока, поэтому будет небольшое различие между реальным и расчетным приращением напряжения. Однако для практических целей эта система работает достаточно удовлетворительно.

Автор: Чарльз Платт

Напряжение, сопротивление и емкость

admin

Добавить комментарий Отменить ответ