Теоретическая вольтамперная характеристика p-n-перехода

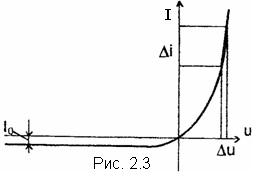
Вольтамперная характеристика (ВАХ) представляет собой график зависимо­сти тока во внешней цепи p-n-перехода от значения и полярности напря­жения, прикладываемого к нему. Эта зависимость может быть получена экспериментально или рассчитана на основании уравнения вольтампер­ной характеристики [2].

При включении p-n-перехода в прямом направлении в результате ин­жекции возникает прямой диффузионный ток

je = je_{n диф}(x_p) =SqD_n (dΔn/dx) |_x=xp,

где S – площадь p-n-перехода, q – заряд электрона, D_n– коэффициент диффузии электронов.

С учётом \(\Delta n(x_{p})=n(x_{p})-n_{p}=n_{p}[exp(\frac{u}{\varphi _{T}})-1]\) прямой ток p-n-пере­хода определяется выражением

\(I=Sq\frac{D_{n}n_{p}}{L_{n}}[exp(\frac{u}{\varphi _{T}})-1]\)

Обозначим \(Sq\frac{D_{n}n_{p}}{L_{n}}=I_{0}\) , эта величина имеет размерность тока, опреде­ляется концентрацией неосновных носителей заряда в базе n_p и называется тепловым током I₀.

Общее выражение для вольтамперной характеристики p-n-перехода записывается в виде

\(I=I_{0}[exp(\frac{u}{\varphi _{T}})-1]\) (2.7)

где I₀ – тепловой ток p-n-перехода, с учётом дырочной составляющей те­пловой ток может быть записан в виде

\(I_{0}=Sq(\frac{D_{n}n_{p}}{L_{n}}+\frac{D_{p}p_{n}}{L_{p}})\) (2.8)

Тепловой ток p-n-перехода зависит от концентрации примеси и темпе­ратуры. Увеличение температуры p-n-перехода приводит к увеличению теплового тока, а, следовательно, к возрастанию прямого и обратного то­ков.

Увеличение концентрации легирующей примеси приводит к уменьше­нию теплового тока, а, следовательно, к уменьшению прямого и обратного токов p-n-перехода.

На рис. 2.3 приведена ВАХ идеального p-n-перехода.

Учитывая, что при Т = 300К, φ_T= 26 мВ, можно сделать вывод, что пря­мой ток очень сильно зависит от прямого напряжения (при увеличении U на 2φ_T мВ прямой ток возрастает в 10 раз). Наоборот, обратный ток при обратных напряжениях, больших 2φ_T мВ, практически перестает зависеть от приложенного напряжения и равен I₀. Реально прямой и обратный токи по величине отличаются на порядки и для них используются разные мас­штабы. Поскольку ВАХ p-n-перехода представляет собой нелинейную за­висимость между током и напряжением, то между малыми амплитудами тока и напряжения (или между малыми приращениями тока и напряжения Δi и Δu) существует линейная связь. В этом случае p-n-переход на перемен­ном токе характеризуют дифференциальным сопротивлением R_ré:

R_ré =du/dI≈Δu/Δi.

Аналитическое выражение r_pn получим, дифференцируя (2.7)

R_ré =φ_T/(I+I₀). (2.9)

При прямом напряжении r_pnмало и составляет единицы – сотни Ом, а при обратном напряжении – велико и составляет сотни и тысячи килоОм.

Дифференциальное сопротивление можно определить графически по характеристике (рис. 2.3, где указаны Δi и Δu ).